稀疏矩阵及其存储格式（COO、CSR、CSC）

Posted on In Views:

在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵；与之相反，若非0元素数目占大多数时，则称该矩阵为稠密矩阵。定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。简单来说,稀疏矩阵就是绝大部分都是0的矩阵,只包含很少的非零值.

封面 [ID:79498766].

稀疏矩阵

例如：

\[ \begin{pmatrix} 1 & 2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 3 & 4 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 6 & 7 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 8 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 9 \\ \end{pmatrix} \]

上述稀疏矩阵非零元素有9个，26个零值，稀疏性是74%。

稀疏矩阵因为绝大部分都是0元素,如果我们仍然按照普通方式存储,无疑会浪费很多空间;同时如果进行运算时,0元素对最终结果也没有帮助,增加了许多无效计算. 因此,我们需要设计出新的存储方式,或者说数据结构来存储稀疏矩阵.比较常见的有：

  • DOK: Dictionary of keys. 将非零元素的坐标 (row, column) 作为key,非零元素值作为value,只存储非零元素值. 可以以任意顺序逐渐构建稀疏矩阵;但是按某种顺序访问非零元素时比较困难. 通常用来构建矩阵,然后再把矩阵转换成别的方式.
  • COO: Coordinate list. 坐标格式. 三个数组row,col,value分别存储非零元素坐标的行,列以及非零值. 理论上稀疏矩阵中的元素在存储时顺序是任意的,但是为了方便元素访问,存储时先按照先左后右,先上后下顺序进行存储(left to right, top to buttom).
  • CSR: Compressed Sparse Row. 压缩稀疏行
  • CSC: Compressed Sparse Column. 压缩稀疏列,和CSR类似.

COO

我们使用三个数组row,column和data分别用来存储非零元素坐标的row_index,col_index,以及数值.比如:

COO

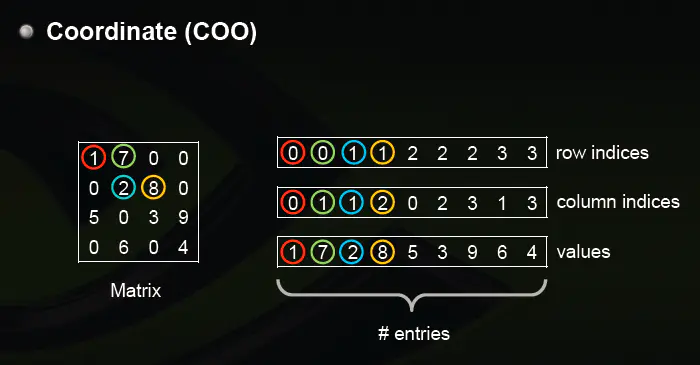
三个数组的长度都是NNO.data[i] (NNO:The number of nonzero.矩阵非零元素个数),在原稀疏矩阵中的坐标为(row[i],col[i]]).

>>> from scipy.sparse import *
>>> 
>>> row = [0,0,1,1,2,2,2,3,3]
>>> col = [0,1,1,2,0,2,3,1,3]
>>> data = [1,7,2,8,5,3,9,6,4]
>>> import numpy as np
>>> coo = coo_matrix((data,(row,col)),shape=(4,4),dtype=np.int)
>>> coo
<4x4 sparse matrix of type '<class 'numpy.int64'>'
    with 9 stored elements in COOrdinate format>
>>> coo.todense()
matrix([[1, 7, 0, 0],
        [0, 2, 8, 0],
        [5, 0, 3, 9],
        [0, 6, 0, 4]])

可以发现,这种存储方式中,row数组和column数组中有一定的重复元素.我们是否可以针对这个冗余特性进一步进行压缩? 之后的CSR,CSC,分别是对row数组和column数组进行了压缩.

CSR与CSC

  • V，用来存储矩阵中的非零元素的值；
  • COL_INDEX，第i个元素记录了V[i]元素的列数；
  • ROW_INDEX, 第i个元素记录了前i-1行包含的非零元素的数量。 进一步，令a=ROW_INDEX[row], b = ROW_INDEX[row+1]，则V[a, b)的行数等于row，再结合COL_INDEX，即可得到非零元素的行数和列数。

\[ \begin{pmatrix} 1 & 2 & 0 & 0 & 0 & 0 & 0 \\ 0 & 3 & 4 & 0 & 0 & 0 & 0 \\ 0 & 0 & 5 & 6 & 7 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 8 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 9 \\ \end{pmatrix} \]

其中 V = [1, 2, 3, 4, 5, 6, 7, 8, 9] COL_INDEX = [0, 1, 1, 2, 2, 3, 4, 5, 6] ROW_INDEX = [0, 2, 4, 7, 8, 9]

假如我们想得到“7”的坐标位置，通过V得到index为6，通过COL_INDEX得到列数为4； 4 ∈ [4,7) ，所以行数为2，最终7的坐标为(2, 4).

CSC同理.